|
ART GÉOMÉTRIQUE ET GÉOMÉTRIE ARTISTIQUE
|
|
INTRODUCTION Inspiré des oeuvres d'Escher et de Vasarely, ce travail s'appuie sur des théories mathématiques récentes alliant la topologie à la théorie des groupes. Vous trouverez d'abord une représentation figurative des 19 familles de pavages du plan ainsi qu'un algorithme de classification. Une seconde partie propose de nombreuses applications aux polygones, cylindres, sphères, spirales logarithmiques, tores et nœuds.
Enfin, dans une
troisième partie, vous pourrez
manipuler
en 3D
quelques solides
pavés. |
|
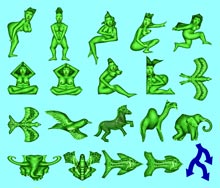
CLASSIFICATION DES PAVAGES DU PLAN Cette classification est définie par la règle suivante: "Deux pavés sont équivalents si on peut passer de l'un à l'autre par une déformation continue" Cette classification des pavages associe pour 15 des 17 groupes cristallographiques un unique type de pavé. Par contre, pour chacun des deux groupes restant (PG et PGG), on peut associer deux types de pavés topologiquement distincts. La classification des pavages du plan, en fonction uniquement des groupes cristallographiques, ne vérifie pas cette règle à cause des groupes PG et PGG. La classification isohedrale, basée sur le nombre d'arcs frontières d'un pavé, ne vérifie pas non plus cette règle, car par déformation continue, un arc peut se réduire à un point. Cette classification algébrique et topologique aboutie alors à 19 familles de pavages du plan.
Les
pavés verts ont toujours le
nombre maximum
d'arcs frontières. L'algorithme
permet de classer chacune de ces
19 familles de pavages du
plan
selon cette règle. |
 |
|
SURFACES 3D Les illustrations présentées ici sont des captures de surfaces 3D plus étonnantes encore: Sur le réseau de spirales logarithmiques, on peut modifier automatiquement le nombre de spirales de chaque couleur, les rapports de similitudes, faire entrer ou sortir les éléphants jaunes au survol de la souris.
Vous observerez
sur cette image qu'il y a
1 spirale jaune
sortante, 17
spirales rouges
sortantes, 18
spirales oranges
entrantes et qu'à chaque tour les éléphants jaunes
grandissent
selon le nombre
d'or. |
|
|
GROUPE P3 |
|
|
GROUPE P6 |
|
|
GROUPE PG1 |
|
|
GROUPE P31M |
|
|
GROUPE P1 |
|
|
GROUPE P3 |
|
|
GROUPE PG2 |
|
|
GROUPE PG1 |
|
|
GROUPE P4G |
|
|
GROUPE P4 |
|
|
GROUPE PMG |
|
|
GROUPE P31M |
|
MODÉLISATION 3D PRINCIPAUX OUTILS
Les
sculptures
présentées |
, déplacées
ou agrandies
en utilisant la barre
d'outils.
|
|
SPHÈRE |
|
|
NOEUD |
|
|
NOEUD |
|
|
NOEUD |
|
Vous trouverez aussi
Contact |